Mass is one of the principal characteristics of physical bodies… and, perhaps, one of the most mysterious. And that is not just because so many people fail to figure out how to lose weight. Scientists have not yet been able to fully explain the phenomenon of mass as such. That is why the prediction and discovery of the particle “in charge”— the Higgs boson — was awarded the Nobel Prize in 2013. However, even without fully understanding its nature, we have already learned to accurately determine the mass of objects in a huge range — from the electron to the whole universe.
What is the weight of an astronaut?
When we stand on electronic scales after a hearty dinner, we do not determine our mass, but only the force with which our body is attracted to the planet Earth. On other celestial bodies, such a weighing device will give different results: for example, on Mars, the same body will weigh almost three times less, on the Moon — six times less. It is easy to guess that in weightlessness traditional balance will show “zero”, regardless of who “stands” on it. So how do the crew of the International Space Station, for example, weigh themselves?

To answer this question, we should call to mind that mass is a measure of the inertia of the body, ie its ability to resist the action of external forces. A heavier (more massive) object undergoes less acceleration than a lighter one (less massive) under the influence of the same force. So, knowing the force’s magnitude and measuring the acceleration of the body, you can use Newton’s first law to calculate its mass. Such an “accelerator” with appropriate sensors is installed on the ISS, and astronauts regularly use it. In reality, the “mechanics” of this device is a bit more complicated, but it provides sufficient accuracy and reproducibility of results.
It is worth noting that since the times when the law of universal gravitation was formulated, there are two types of mass in physics. We’ve just told you about the first — the inertial mass. The second one —the gravitational mass — reflects how strongly a body attract other bodies under the action of universal gravitation. For a long time scientists have been trying to find out whether the magnitudes of these two masses for the same body always coincide or maybe they can differ under some circumstances. Only in the twentieth century, after the advent of Einstein’s Theory of Relativity, was the “mass paradox” partially explained. The difficulty in studying this question, among other things, is due to the fact that for large bodies (stars, planets, and their satellites) we can mostly measure only the gravitational mass — the lever with which Archimedes wanted to lift the Earth, unfortunately, exists only in imagination of scientists and artists.
Cavendish’s experiment
The British physicist Henry Cavendish was the first to try “weighing” the Earth. In a series of experiments carried out in 1797-1798, he used an improved torsional pendulum with a pre-measured index of elasticity to record the displacement of the smaller metal balls attached to its ends as two much heavier and larger lead balls (weighing 158 kg each) approached. Knowing the force with which small spheres are attracted to large ones and large spheres are attracted to the Earth, the scientist was able to calculate the average density of our planet, and got a figure of 5.448 ± 0.033 g/cm2 (this is less than one percent different from the currently determined value). This result allows us to conclude that our planet consists mainly of metals, while water and rocks constitute relatively small share in its composition.
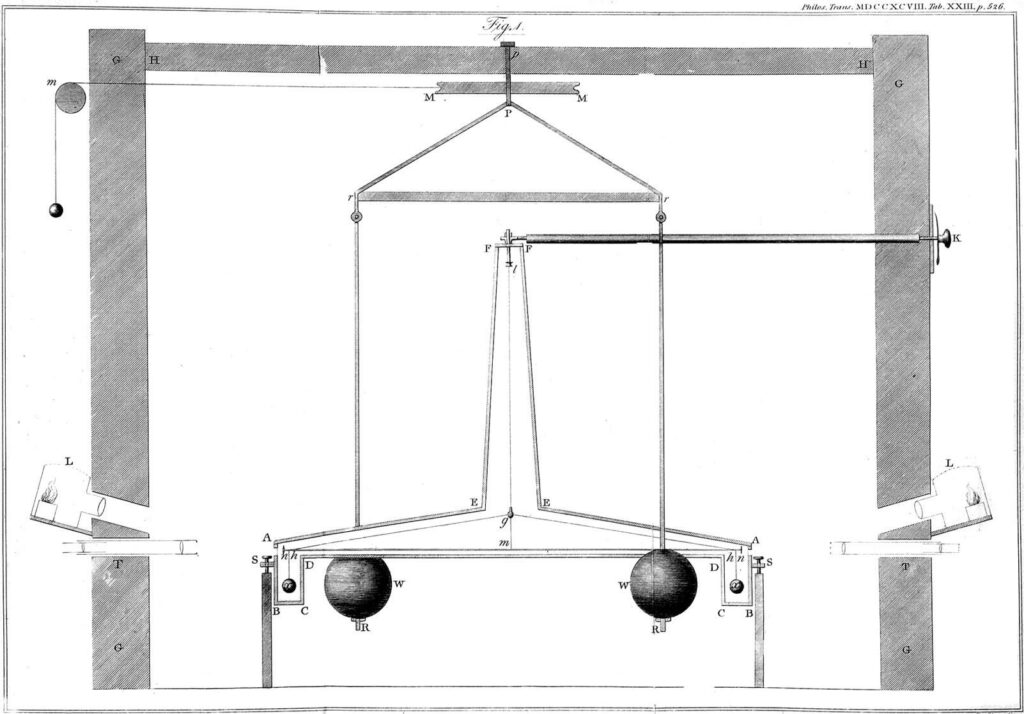
Since the magnitude of the Earth’s radius (and hence its volume) was already known in Cavendish’s time, it was easy to calculate its mass, and knowing the acceleration of free fall near the Earth’s surface, we can learn the value of the gravitational constant — an important component of the law of universal gravitation. Further refinement of this value is related to the study of the Moon’s motion and the measurement of the average distance to it. And this, in turn, allowed extrapolating the methods of “weighing” to the Sun and other planets in the solar system.
Using satellites
Keep in mind that the gravitational mass determines how strongly two objects are attracted to each other, being at a certain distance. This force, by the way, can be calculated knowing the orbiting period of the planet’s satellite (natural or artificial) and the average radius of its orbit. At the end of the XIX century, the distances from all the planets to the Sun were already known with acceptable accuracy, thanks to which it was possible to determine the mass of our central star — it constitutes mind-bending 2 × 1030 kg (two with thirty zeros). In the same way, all the planets with satellites were more or less accurately “weighed”. The mass of Mercury and Venus was estimated by the gravitational perturbations they exert on other bodies in the solar system. Its exact magnitude became known when space probes approached these planets.
Estimates of the mass of dwarf planets, comets and asteroids are still not very accurate — except for those visited by automatic probes. Even when those Earth’s envoys carried out research from flyby trajectories, the force of gravity of small bodies caused probes to deviate slightly from the “undisturbed” path and change their speed. Those parameters were determined through Doppler frequency shift of onboard radio transmitters, which allowed calculating the mass of the object.

Another method of determining the approximate mass of asteroids and cometary nuclei is to measure the speed of their rotation around their own axes. Since most of them are piles of fragments held together almost exclusively by gravity, such a body must have a mass not lower than a certain limit, lest it is scattered by centrifugal forces.
Interestingly, ballistics specialists who calculate the motion of spacecraft do not use the masses of celestial bodies in their calculations. It is more convenient for them to use an index called “gravitational parameter” — the product of the mass of the planet (star, asteroid, etc.) and the gravitational constant. This parameter can be measured up to the 9th significant digit or even more accurately (for example, for the Sun this value is known up to the 12th significant digit, and it has even been possible to register its gradual decrease due to loss of solar mass). The fact is that many years after the discovery of the law of universal gravitation, scientists have not been able to determine with sufficient accuracy the basic constant that is part of its formula. This is due, among other things, to the fact that gravity is the weakest of all known types of interaction between physical bodies.
The mystery of the Milky Way
When astronomers realized that the Sun is part of a huge stellar system, later named galaxy, they began looking for ways to weigh it. At first, this was impossible because we did not know the speed of rotation of our star around the galactic center, or even its position relative to it (for some time it was believed that the Sun is located somewhere near the center). It was not until the 1930s that the American astronomer Harlow Shapley roughly determined our position and made the first estimates of the size of the Milky Way, but determining its mass was still a long way off.
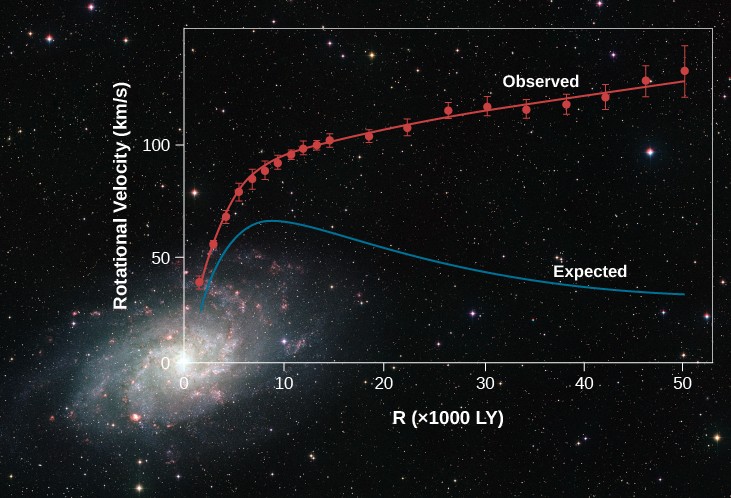
The main problem is that the duration of one rotation of the Sun around the galactic center exceeds 200 million years, and the first telescopes were invented just about four centuries ago. Even less time has passed since the invention of spectroscopes, which allowed us to measure the radial velocities of stars and get a general picture of their motion in the galaxy. This is where the first problems arose. In the solar system, the average speed of an object orbiting around a central body is always inversely proportional to the square root of the mean radius of that orbit. Within the Milky Way, this law also “works”… to a certain distance. But, beginning with about 10,000 light-years from the galactic center, the linear velocities of stars and their clusters almost cease to change. It turned out that similar “discrepancies” are observed in many other galaxies. It was not possible to explain them by already known phenomena or processes. Astronomers then hypothesized the existence of a hitherto unknown massive “attracting” agent, inaccessible to observations in any range of electromagnetic waves. That’s how we learned about the mysterious “dark matter”.
In general, by studying the dynamics of a large number of stars, the “behavior” of interstellar matter and dwarf galaxies which are located near the Milky Way and considered its satellites, scientists have determined that the total mass of our multistellar system within a radius of 130,000 light-years from its center is about one and a half trillion solar masses, or 3 × 1042 kg (three with 42zeros). And this is not the largest galaxy in the universe!
Weight everything
At first glance, it may seem that it is impossible to determine the mass of our infinite universe — after all, is not its mass infinite as well? But this is not quite so. Although our world has no physical limit (and, as cosmologists have shown in the 1920s, it is constantly expanding), the amount of matter that has mass is limited and even gradually decreases — due to “burnout” in thermonuclear reactions in the bowels of stars.

Of course, we cannot use the “Archimedes lever” to weigh the universe. Neither can we determine its mass by the speed of bodies orbiting around it (because all known bodies are inside). However, the very fact of its existence makes it possible to set certain limits on the “world mass”: had it been too large, all massive bodies would have been attracted to each other in the early stages of world evolution.
To determine the lower limit, astronomers have tried to “weigh” all the matter within the reach of modern instruments of observation — stars, galaxies, intergalactic gas clouds. The calculations were getting ever more complicated as the new components appeared, that are impossible (or near impossible) to see, but they still make up considerable part of the “mass balance”: exoplanets, “dark matter”, neutrinos…

The most detailed information was obtained using the American WMAP satellite (Wilkinson Microwave Anisotropy Probe) and the European Planck Observatory, which studied the relic microwave radiation — the “remnants of the flash” of the Big Bang, which formed our world. Small variations in this radiation, due to the initial inhomogeneities of primordial matter and the passage of light through later large-scale cosmological structures, contain data on the mass of objects encountered by relic photons. After analyzing the results, astronomers calculated the average density of the universe: it is equivalent to the mass of six protons per cubic meter.
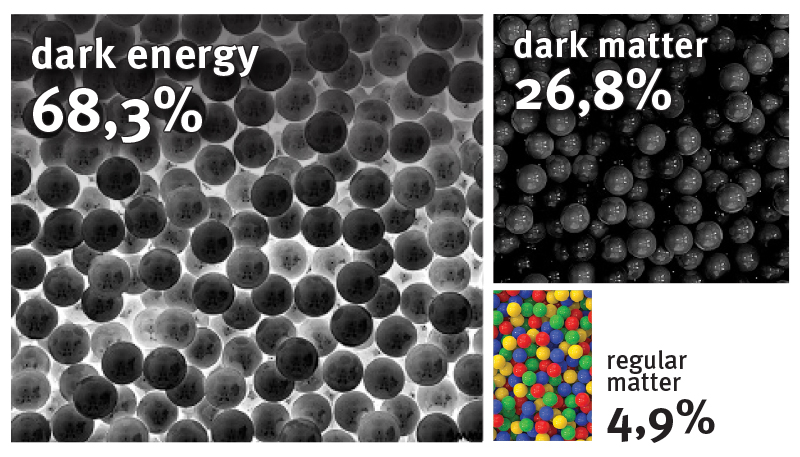
In fact, this value is technically the density of energy (it can be “converted” into mass by the well-known Einstein’s formula E = mc2, and such transformations do occur constantly in the real world). It contains not only “visible” matter, also known as “baryon matter”, but also the already mentioned dark matter, and an even more mysterious component of the universe, which causes the universe to accelerate in its expansion — dark energy.
If we multiply this density by the volume of space from which light has already reached terrestrial observers in 13.8 billion years (this is the estimated age of the universe), we get 1053 kg — unity with 53 zeros. Even if we count just the baryon matter, which constitutes only 5% of the universe, according to the latest data, the figure obtained is still huge. Of course, all these figures are going to be updated, but it is unlikely that the new ones will differ from the already known more than by one order of magnitude. And knowing the total mass of our world, scientists will better understand its evolution — both in the past and in the projection for the future.