On 14 March (3.14 in the American date system), the world celebrates the Day of the Number “pi” — this is the name of the Greek letter π. Its first three significant digits, 3.14, are probably known to everyone who is at least a little familiar with mathematics. In fact, there are an infinite number of them, and scientists want to know as many of them as possible. Why do they need to know them and how did our ancestors calculate this number?
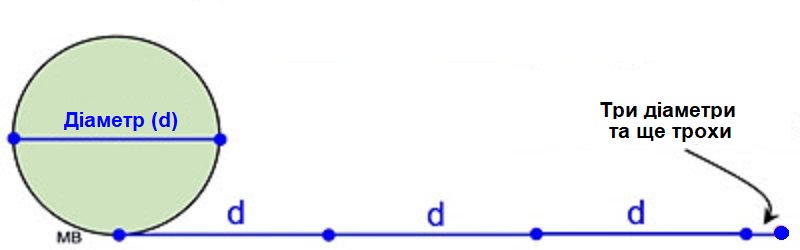
The ancient Egyptians noticed that the ratio between the length of a circle and its diameter is a constant: if you “unwrap” a rope wrapped around a cylinder of arbitrary diameter, its length will be equal to three diameters of this cylinder and a little more. The value of this “little bit” has long puzzled mathematicians. At first, it was quite enough to assume that it “fits” into the diameter seven times. But later, when more precise calculation methods became available, it became clear that things were not so simple.
If we convert 1/7 to a decimal, we get 0,142857142857142857… – an endless sequence of six digits that repeats periodically. This repetition of a longer or shorter “digit chain” is characteristic of all rational fractions that are formed by dividing any two integers by each other. Since in everyday life we use the decimal system based on the prime numbers 2 and 5, dividing by them, their powers, or the product of their arbitrary powers will give a finite sequence of digits, such as 0.04 or 3.75. All the others will form so-called periodic fractions.
Ancient Greek scientists began to calculate the value of the most important constant as an intermediate value between the lengths of the perimeters of regular polygons described and inscribed in a circle of unit radius. By the way, this is where the designation π originated, which was originally used to denote the length of half the perimeter. It was its ratio to the radius denoted by the letter ρ that gave the desired value. For a long time, it was denoted as π/ρ. The “lonely” letter π was first used in 1706 by the English mathematician William Jones in his work Synopsis Palmariorum Matheseos, after which it became common. But let’s go back to ancient Greece.
The half-perimeter of a hexagon inscribed in a circle of unit radius is three, and the half-perimeter of a square drawn around it is four. Obviously, the more angles a polygon has, the closer it will be to a circle, and its semi-perimeter will be to the number π. But there was one problem: to calculate the length of a side of such a polygon, you had to use the square root function (Pythagoras’ theorem was already known). The result of the calculations was not rational but irrational fractions — no sequences of digits were repeated. And the calculation of such quantities took a lot of time and effort. Therefore, scientists decided for a while to limit themselves to the lower and upper limits of π, expressed as ratios of relatively small numbers. The famous Archimedes, around 250 BC, used the already known value 22/7 as the latter, and proposed the fraction 223/71 for the “lower limit”.
More than 100 years later, Claudius Ptolemy in his major work Almagest indicated the value of 3.1416, which is still generally sufficient for most household needs. The situation with mathematics was much worse in the East. At the beginning of the modern era, the Chinese used the 142/45 approximation, which was later improved to 3.1547. It was only in 265 that the Chinese scientist Liu Hui also reached the same value as Ptolemy’s, calculating the length of a half-perimeter of a 3072-gon. Around 480, the court astronomer Zu Chunzhi calculated the number π to 7 decimal places and proposed a very good, and most importantly, easy-to-remember ratio of 355/113.
Further progress in this direction began with the onset of the European Renaissance. It gave impetus to the development of mathematical science and computational methods. In the seventeenth century, mathematicians James Gregory and Gottfried Leibniz proposed using infinite regular converging number series to calculate the number π. The simplest of them is: π/4=1–1/3+1/5–1/7+1/9–1/11+1/13–1/15…

Later, more convenient series appeared — they made it possible to calculate not only the value of π, but also very important trigonometric functions with increasing accuracy. At the same time, some mathematicians wondered if the number π was still rational and, after a certain digit, would “give out” a sequence that repeated the one already passed? Proving the opposite was not an easy task. It took until 1768 for the Swiss scientist Johann Lambert to do so. And in 1882, the German mathematician Ferdinand von Lindemann proved that π is a transcendental number, meaning that it is not a rational degree of any rational fraction.
However, the purely computational component was slowed down for a long time by the lack of the necessary technical base: it became increasingly difficult to add and subtract long sequences of digits by hand, and each subsequent digit required more and more time to calculate. In the middle of the nineteenth century, the number of known digits in π reached five hundred, and over the next hundred years it grew only slightly. Everything changed with the advent of electronic computers. In 1949, American mathematicians John Rentsch and Levi Smith calculated 1120 significant digits on one of the first calculators that could already be called a “desktop”. In 1973, almost simultaneously with the birth of the four billionth inhabitant of the Earth, humanity celebrated the millionth digit of the number π.

As of 2022, the number of known signs in this number has reached one hundred trillion, and this figure continues to grow. Why do scientists need this? First, such calculations are a good “test material” for improving computing methods and, of course, computer technology. Secondly, irrational and transcendental numbers with their unpredictable digital sequences help encryptors to encode secret messages (and cryptanalysts can use them to decrypt them). Finally, physicists and cosmologists have always sought to determine as accurately as possible all the constants of our world that determine its properties and future fate. The number π is one of these constants, the advantage of which is that it does not require complex observations and measurements to refine it — just careful calculations are enough.
And if someone wants to study this magic number to the 50th decimal place, it is not difficult: 3,14159265358979323846264338327950288419716939937510…
Also on March 14, the world celebrates the 145th anniversary of Albert Einstein’s birth.

