14 марта (3.14 в американской системе записи дат) мир отмечает День числа «пи» — так читается название греческой буквы π. Три его первых значащих цифры 3,14 знают, пожалуй, все, кто мало-мальски знаком с математикой. На самом деле их там бесконечное количество, и ученые стремятся узнать их как можно больше. Зачем это им и как это число представляли себе наши предки?
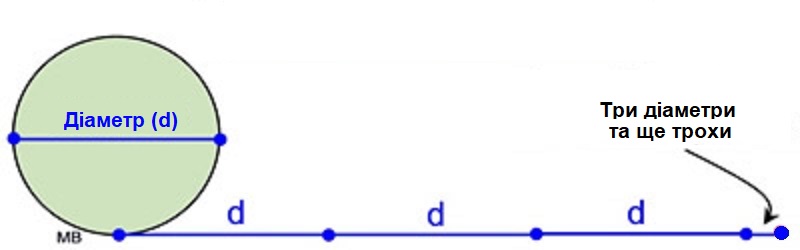
Еще древние египтяне обратили внимание, что соотношение между длиной окружности и ее диаметром является постоянной величиной: если «развернуть» веревку, обмотанную вокруг цилиндра произвольного диаметра, ее протяженность будет равна трем диаметрам этого цилиндра и еще немного. Величина этого «немного» долго не давала покоя математикам. Вначале было вполне достаточно считать, что она «укладывается» в диаметр семь раз. Но позже, когда появились более точные методы вычислений, стало ясно, что не все так просто.
Если перевести 1/7 в десятичную дробь, мы получим 0,142857142857142857… — бесконечную последовательность из периодически повторяющихся шести цифр. Такое повторение более длинной или короткой «цифровой цепочки» свойственно всем рациональным дробям, получающихся делением друг на друга произвольных целых чисел. Поскольку в быту мы пользуемся десятичной системой, базирующейся на простых числах 2 и 5, деление на них, их степени либо произведение их произвольных степеней даст конечную последовательность цифр типа 0,04 или 3,75. Все остальные будут образовывать так называемые периодические дроби.
Древнегреческие ученые взялись вычислять значение важнейшей константы как промежуточную величину между длиной периметров правильных многоугольников, описанных и вписанных в круг единичного радиуса. Кстати, отсюда и происходит сам символ π, которым первоначально обозначали длину половины периметра. Именно ее отношение к радиусу, обозначенному буквой ρ, и давало нужную величину. Долгое время ее так и обозначали — π/ρ. «Самостоятельную» букву π начал использовать в 1706 году английский математик Уильям Джонс в своем труде Synopsis Palmariorum Matheseos, после чего она уже стала общепринятой. Но вернемся в Древнюю Грецию.
Полупериметр шестиугольника, вписанного в окружность единичного радиуса, равен трем, а квадрата, описанного вокруг нее, — четырем. Очевидно, чем больше углов у многоугольника — тем сильнее он будет «приближаться» к кругу, а его полупериметр — к π. Но тут появилась одна неувязка: для вычисления длины стороны такового многоугольника приходилось употреблять функцию квадратного корня (теорема Пифагора была уже известна). Результатом расчетов стали уже не рациональные, а иррациональные дроби, в которых никаких последовательностей цифр не повторялось. Да и вычисление таких величин занимало много времени и усилий. Поэтому ученые решили обойтись нижним и верхним пределом значения π, выраженными соотношениями относительно небольших чисел. Знаменитый Архимед около 250 года до н.э. в качестве последнего использовал уже известную величину 22/7, а для «ограничения снизу» предложил дробь 223/71.
Примерно через сотню лет Клавдий Птолемей в своем главном труде «Альмагест» указал значение 3,1416, которое и сейчас вполне подходит для большинства бытовых нужд. Значительно хуже дела с математикой обстояли на Востоке. Еще в начале новой эры китайцы пользовались аппроксимацией 142/45, позже улучшенной до 3,1547. Лишь в 265 году китайский ученый Лиу Гуй вышел на то же значение, что и Птолемей, вычислив длину полупериметра 3072-угольника. Около 480 года придворный астроном Цзу Чунчжи вычислил число π до 7-го знака после запятой и предложил очень неплохое, а главное — легкое запоминающееся соотношение 355/113.
Дальнейший прогресс в этом направлении начался с наступлением Европейского Возрождения. Оно дало толчок развитию математической науки и вычислительных методов. В XVII веке математики Джеймс Грегори и Готфрид Лейбниц предложили использовать для расчета числа π бесконечные регулярные сходящиеся ряды. Самый простой из них выглядит следующим образом: π/4=1–1/3+1/5–1/7+1/9–1/11+1/13–1/15…

Потом появились и более удобные ряды — они позволили со все более высокой точностью вычислять не только значение π, но и очень важные тригонометрические функции. Параллельно некоторые математики задались вопросом: а вдруг число π все же рациональное и после какой-то цифры «выдаст» последовательность, повторяющую уже пройденную? Доказательство противоположного оказалось нелегким делом. Это сделал только в 1768 году швейцарский ученый Иоганн Ламберт. А в 1882-м немецкий математик Фердинанд фон Линдеман доказал, что π — число трансцендентное, то есть оно не является никакой рациональной степенью ни одной рациональной дроби.
Но чисто вычислительная составляющая долго тормозилась отсутствием необходимой технической базы: складывать и вычитать «вручную» длинные последовательности цифр становилось все труднее, и каждый следующий знак требовал все больше времени для расчета. В середине XIX века количество известных цифр в числе π «дотянули» до полутысячи, и за следующую сотню лет оно возросло несущественно. Все изменилось с появлением электронных вычислительных машин. В 1949 году на одном из первых калькуляторов, который уже можно было назвать «настольным», американские математики Джон Ренч и Леви Смит вычислили 1120 значащих цифр. В 1973-м, почти одновременно с рождением четырехмиллиардного жителя Земли, человечество праздновало миллионный знак числа π.

По состоянию на 2022 год количество известных знаков в этом числе удалось довести до ста триллионов, и этот показатель продолжает расти. Зачем это ученым? Во-первых, такие расчеты являются хорошим тестовым материалом для совершенствования методики вычислений и, конечно, компьютерной техники. Во-вторых, иррациональные и трансцендентные числа с их непредсказуемыми цифровыми последовательностями помогают шифровальщикам кодировать секретные послания (соответственно, криптоаналитики могут использовать их для расшифровки). Наконец, физики и космологи всегда стремились как можно точнее определить все константы нашего мира, которые влияют на его свойства и судьбу. Число π — одна из таких констант, преимущество которой заключается в том, что для ее уточнения не требуются сложные наблюдения и измерения — достаточно тщательных вычислений.
А если кому-то захочется выучить это магическое число до 50-го знака после запятой — это совсем несложно: 3,14159265358979323846264338327950288419716939937510…
Также 14 марта мир отмечает 145-ю годовщину со дня рождения Альберта Эйнштейна.
Только самые интересные новости и факты в нашем Telegram-канале!
Присоединяйтесь: https://t.me/ustmagazine


