We know that supermassive black holes in the centers of galaxies can have masses billions of times greater than the Sun. However, is there a limit beyond which they cannot be larger? This question is not as simple as it may seem.

The size of black holes
Black holes are regions of space in which the force of gravity is so great that to go beyond them, one must move faster than light, which is impossible. The boundary of such a region is called the event horizon.
Theoretically, black holes can be as small as desired, up to the Planck limit of 1.61*10-35 m. However, in the modern Universe, no processes could produce black holes with a mass less than 2 solar masses.
They existed at the very beginning of the Universe. Still, most of the primordial black holes that formed then should have already disappeared due to a process known as Hawking radiation. It is the spontaneous birth of particles and antiparticles near the event horizon, one of which falls on the black hole, and the other flies away, taking with it some of the energy and thus the object’s mass.
And while the minimum size of black holes is more or less clear, the maximum size is much more complicated. The objects formed by supernova explosions must have a mass less than that of the stars with which they occur. This means that the maximum mass is several tens of solar masses, which is in good agreement with available observations.
However, we must also take into account the fact that after formation, these objects can actively absorb matter and merge. As a result, something called an intermediate-mass black hole is formed, which is 100-100,000 times larger than the solar mass. Theoretically, it should not be much different from its smaller relatives, but scientists do not know how much this is true, because so far none of them has been proven to exist with complete certainty.
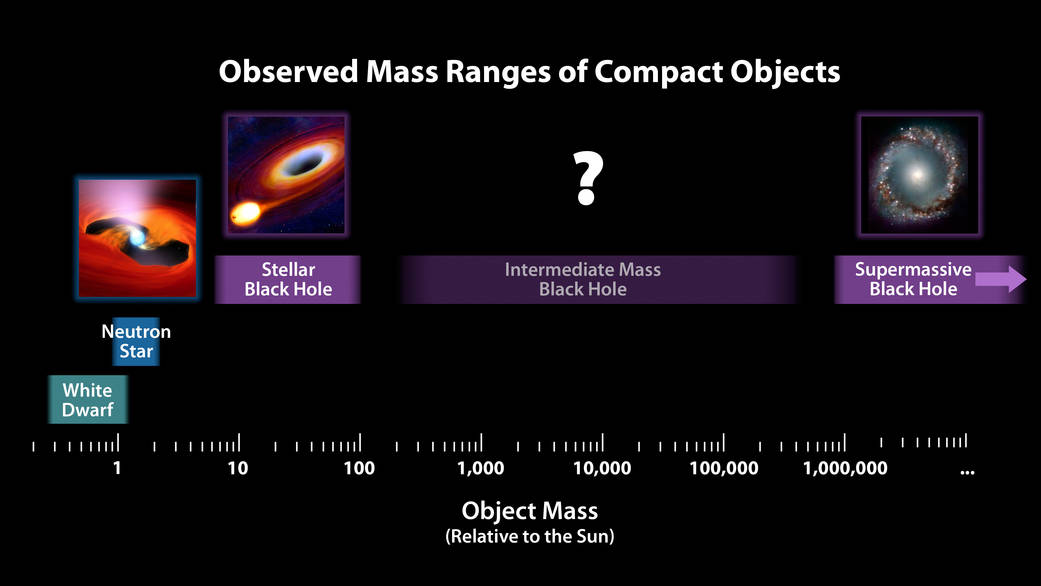
Supermassive black holes
But we know for sure that there are black holes of much larger size, which scientists call supermassive. We know for sure that these objects exist because one of them is located right in the center of the Milky Way galaxy, only 27 thousand light-years away.
The black hole itself, called Sagittarius A*, is invisible in any part of the spectrum. However, astronomers can see large stars orbiting it at a distance of only a few tens of light-years. Their behavior is due to the gravitational influence of an extremely large body, whose mass is 4.3 million times greater than the solar mass.
However, scientists know that this is not the limit. Because there are also supermassive black holes in the center of other galaxies, and they can be much larger than Sagittarius A*. Their mass can be tens of billions of times larger than our star.

Methods of mass estimation
So which black hole is the largest and is there any upper limit to the mass of these objects? The answer to this question is not as simple as it seems. To begin with, it should be noted that using the same method as in the case of Sagittarius A*, scientists have determined the masses of black holes in only a few galaxies closest to us.
However, they make up only a small fraction of the systems we know to have a supermassive black hole at their center. Most of them are accessible for observations because they are not as quiet as Sagittarius A*. They actively absorb gas and dust from the environment and eject some of it outward in the form of jets. They are so powerful that they can be seen from distances of billions of light-years.
Scientists can easily tell by how powerful these rays are that the objects that gave rise to them are really big, but it is impossible to determine their mass exactly. Because we can’t see stars that orbit directly around them.

Therefore, in such cases, scientists use other methods. For example, you can try to observe dust and gas right next to the place where the black hole is supposed to be. Of course, we can’t see the motion caused by its gravity. However, because this substance radiates, we can see its spectrum. All we need to do next is figure out how the lines in the spectrum are shifted due to the Doppler effect, and use them to determine the speed of motion, the force of gravity, and the mass of the invisible object.
Another way is to track the movement of stars, which is much easier to see on the scale of the entire galaxy than in a small central region. According to the parameters of the velocity distribution in a star system, it is possible to determine whether there is a massive single object in its center or not. In particular, it is believed that there is a linear relationship between the velocity dispersion of stars in a galaxy and the mass of a black hole in the center.
There are many methods, but they have one huge drawback. The results obtained with their help not only have a large discrepancy. They also contradict each other. That’s why the answer to the question of which black hole is the most massive looks somewhat contradictory.

Which black hole is the “heaviest”?
The main candidate for the title of the most massive black hole is SDSS J140821.67+025733.2. This is an extremely bright quasar in the constellation Virgo. Its mass was initially estimated at 196 billion solar masses, but was later corrected and is now believed to be “only” 112 billion times greater than that of our Sun.
Next is Phoenix A, also a quasar located in the giant Phoenix galaxy cluster. It is believed that the mass of this black hole is 100 billion solar masses. Then there is IC 1101 with a mass of 97 billion solar, SDSS J150848.79+605551.9 with a mass of 68 billion solar, and 4C+74.13, whose mass is estimated at 51 billion solar.
The supermassive black hole TON 618 is also mentioned as the “heaviest”. The fact is that its mass was previously estimated at 66 billion solar masses, but later studies have made it possible to estimate it at 40.7 billion solar masses.
The problem with all these numbers is that they were obtained using very indirect methods. The conclusions were based either on the study of certain lines in the quasar’s spectrum or on the size of the central region of the galaxies in which they are located. Therefore, there is a serious suspicion that all these estimates may be overestimated by several or even dozens of times.

In addition, there is a theoretical estimate of the maximum size to which a supermassive black hole could grow over the 13.7 billion years that the Universe has existed. It is only 50 billion solar masses and is determined by the maximum amount of matter that a black hole can absorb per unit of time, because when this value is reached, the radiation coming from it and the processes of star formation in the accretion disk balance the flow of matter caused by gravitational forces.
More precisely, black holes with a mass of up to 270 billion solar masses can theoretically exist. However, for this to happen, they need to rotate at the highest possible speed. However, none of the studied supermassive black holes are even close to spinning that fast.
So, the question arises: is this theoretical limitation wrong, or is the mass of the largest objects estimated? There is no consensus on this, but most scientists are reasonably inclined to the second option.
There is a third possibility, which is not taken into account in all the previous theoretical accounts. Just as stellar-mass black holes can merge to form intermediate-mass objects, their supermassive relatives can grow by merging. In this case, all theoretical restrictions on their maximum size become irrelevant.

However, supermassive black holes can only merge when galaxies collide. And how often and how fast this happens remains a controversial issue. Therefore, it is impossible to say for sure how much all this affects the evolution of these objects.
Cosmic Horseshoe Galaxy
That is why the recently published article on the determination of the mass of the black hole in the center of the Cosmic Horseshoe galaxy looks very interesting. The point here is not in the obtained mass value of 36 billion solar masses, which, at least at first glance, is not a record, but in the way it was determined and the conclusions that were obtained during the study.
The Cosmic Horseshoe is not a single galaxy, but a complex object that is a perfect example of the gravitational lensing effect. The theory of relativity predicts that the gravity of a massive body should bend the rays that pass through it. Therefore, if there is another massive galaxy behind one, the light rays will bend around it and form a distorted image in the form of duplicate objects, arcs, or rings.
The existence of the gravitational lensing effect was predicted several decades ago, but scientists began to discover such objects in practice only in the 21st century. Thus, the Cosmic Horseshoe, discovered in 2007, was one of the first proofs that Einstein was right about this.
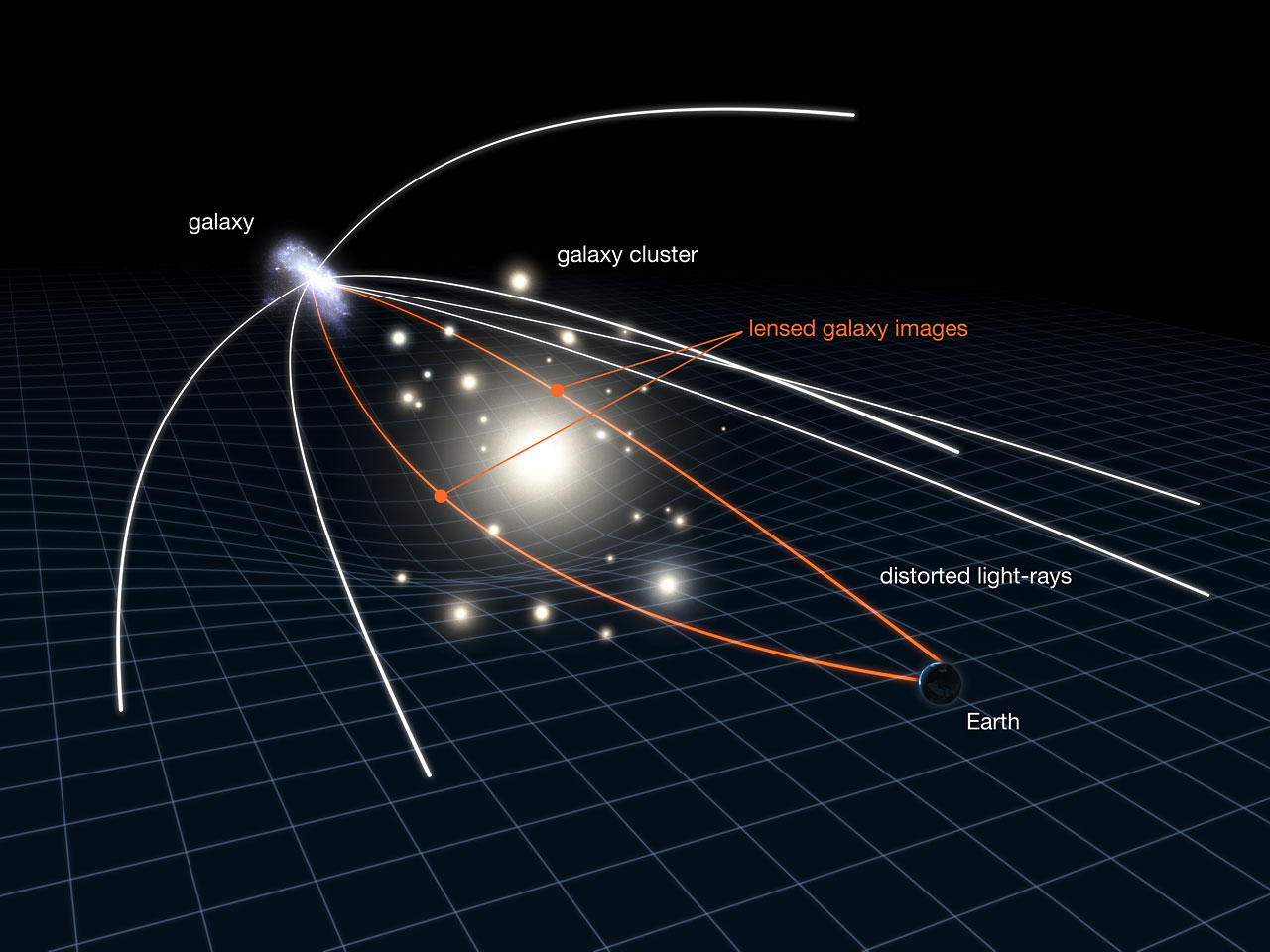
The Cosmic Horseshoe is interesting because it consists of not two, but three objects at once. One of them is the giant and very bright red elliptical galaxy LRG 3-757. It is in the foreground and creates the effect of a gravitational lens.
There are two more star systems beyond LRG 3-757. The light from one of them is strongly distorted by a gravitational lens. We see it as a bright arc, which gave the name to the Cosmic Horseshoe.
But besides it, the images show another star system whose image is distorted but not stretched into an arc. The distances to both lensed objects are known, so the scientists used this fact to test the accuracy of the methods for determining the masses of black holes on the object in the center of LRG 3-757.
Initially, astronomers used an indirect method and determined the mass of the black hole by the dispersion of the rotational speeds of stars in the galaxy. And then they built several models of the gravitational lens, based on assumptions about the mass of a point object in the center, or its absence. And then they looked at which of the models most closely matched what was observed and concluded what size the object was.

Thus, the scientists obtained two independent estimates of the black hole’s mass, which were very close, but the value obtained from the gravitational lens simulation was slightly higher.
This led them to believe that the relationship between the dispersion of stellar velocities in a galaxy and, in general, its mass and the mass of the black hole may not be as linear as it is thought. That is, with an increase in the mass of the galaxy, the black hole in its center should be larger than expected so far.
So how massive can black holes be?
The result obtained in the study is really interesting from the point of view of the discussion about the largest black holes. Because before that, a balanced check of the results mostly showed that the authors of sensational discoveries of the “most massive black holes” tend to overestimate their size. And even the idea that mergers could significantly increase the chance of exceeding the theoretically predicted limit of 50 billion solar masses did not seem very reasonable.
The new study can be viewed as an argument in favor of the fact that very large numbers in weight estimates may still be true. However, it is worth remembering that this study is not the last one, and arguments in favor of this or that opinion will appear repeatedly.
In any case, the estimate of 36 billion solar masses obtained by two independent methods is one of the most reliable that scientists have for the most massive objects in the Universe. Quite a few black holes have been discovered in the range of 30-40 billion solar masses, i.e. 8-10 thousand times larger than Sagittarius A*. That is, at least this mass range can be considered real.
The only question is how much higher are the estimates that scientists currently have for SDSS J140821.67+025733.2, Phoenix A, and other largest black holes. If their masses are exaggerated by only 2-3 times, this means that they fit well within the range mentioned above. In this case, neither the theoretical limit on the mass of black holes needs to be revised nor the question of how frequent their mergers are raised.
However, if the estimates of black hole masses are exaggerated by no more than a few tens of percent, this means that the maximum of 50 billion Sun masses is not the maximum, and it needs to be explained somehow. Thus, the debate over the size of supermassive black holes continues.


